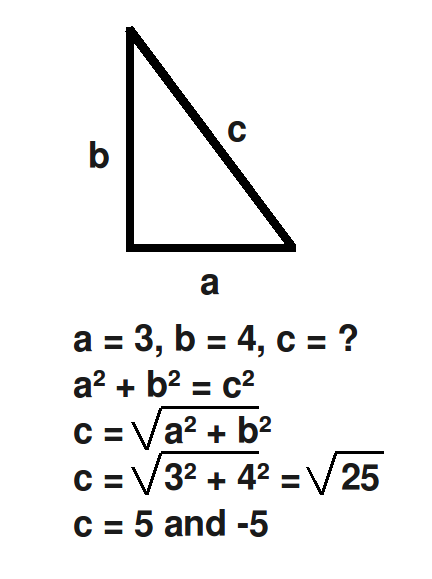Originally I wanted to call this episode “Does Math Reflect Reality?” or “The Limits of Math” but then I decided on the title “How Math can be Right and Wrong at the Same Time” – it sounds more, how shall I say… captivating.

And yes, I’m going to start off with a little mathematical task to illustrate that mathematical solutions do not always correspond to reality. Let’s start off simple. Certainly you remember the Pythagorean Theorem. If the length of two sides of a right triangle are known, then it’s easy to calculate the third side: a²+b²=c². I’m going to show you now an example using this formula.

Lets use some simple values to make calculation easy. If the lengths of the two legs of the right triangle a and b have the values 3 and 4 (a=3 and b=4), what is the length of the hypotenuse c?
3²+4²=c²
9+16=c²
25=c²

Well, what is c then? We have to calculate the square root of each side. If you say c=5, then I have to say, only half correct! There are of course two answers for c, namely 5 and -5. So there are two answers for the length of the hypotenuse of the triangle. Mathematically, the length of the hypotenuse could also be less than 0, it could also be negative. You are going to say, that the length can not be a negative value. And you are, of course, right. But the question goes much deeper. It is you, the person, who has to actively evaluate the results of a calculation to check if the result corresponds to reality. The result of a mathematical calculation may be mathematically correct but still “wrong” when we try to apply it to the “real world”.

There is also a second example, but here I’m not going to use any formulas. This example is from physics, from Albert Einstein’s Theory of Relativity. You already heard that the fastest maximum speed is the speed of light. I know, I know, some of you are going to complain now and say, this is not true, because the universe itself is able to expand faster than the speed of light. Still, inside space, inside the universe, the maximum speed is the speed of light. This limit does not apply to the forming of space by an expanding universe, but actually this is not the main issue I want to talk about.

Just like the triangle example, the equations of Einstein’s Special Theory of Relativity offer several possible solutions. One of these solutions corresponds to the physical world that we all know. This is the “correct” one. There is, however, another solution as well, and this one is really kind of strange. The theory also predicts the existence of so-called Tachyons. Now, what are they? Tachyons are hypothetical particles which are able to travel faster than the speed of light, as a matter of fact, you are not even able to slow them down below the speed of light. Tachyons also possess some other strange characteristics. One of these characteristics is that they lose energy the faster they go. Normally we have to invest energy to make something go faster. You need more fuel to make a car go faster, for example. But tachyons are different. When their energy is 0, they have even infinite speed.

The question is now, do they really exist? No. They are a merely a product of a mathematical calculation, without any connection to reality. Researchers tried to identify Tachyons, but so far were not successful. They are purely hypothetical particles. Just like the negative length in the triangle example, tachyons only exist in the world of math. Of course you can always say that maybe there are parallel universes in which these particles can exist. But this is pure speculation and not even scientifically verifiable or falsifiable.

“This is all very interesting”, you are hopefully going to say, “but where is the connection to the Theory of Knowledge? Where’s the Knowledge Issue?” Glad you are asking.

The example of the triangle and Tachyons illustrate that mathematical results may not always reflect or model reality. In my view mathematical results require interpretation as well. I claim that interpretation of experimental results is not only a requirement in the natural sciences. Interpretation of primary and secondary sources is not only an important component when doing history. Interpretation not only plays an important role when analyzing qualitative or quantitative data in the human sciences. I claim that even the results of mathematical calculations need to be interpreted whether they correspond to the “real world” or not. And if interpretation also plays a role in math, I’m asking myself, could it be that different people interpret mathematical results differently? How do we know which result is the correct one? To what extent does math then require empirical verification as well?

In conclusion. the above examples illustrate two sides or theories of truth, correspondence and coherence: The mathematical results, including the negative length and the Tachyons are true with themselves, they fulfill the coherence criterion. Purely mathematically, a negative length and Tachyons are not contradictory. They are true by coherence. However, the some results do not correspond to reality, even though the math itself was done correctly. The result therefore does not meet the correspondence theory of truth.

Albert Einstein seemed to be aware of this issue as well:

Mathematics are well and good but nature keeps dragging us around by the nose. Albert Einstein