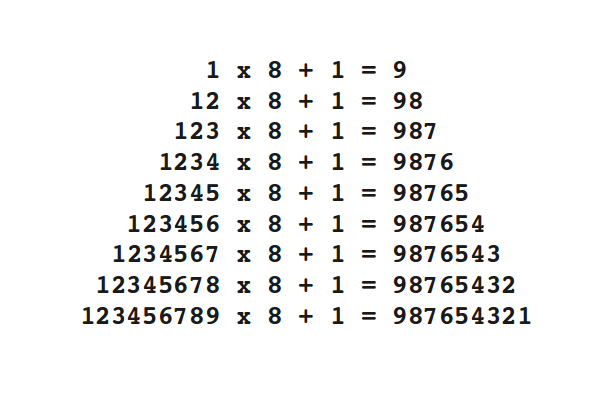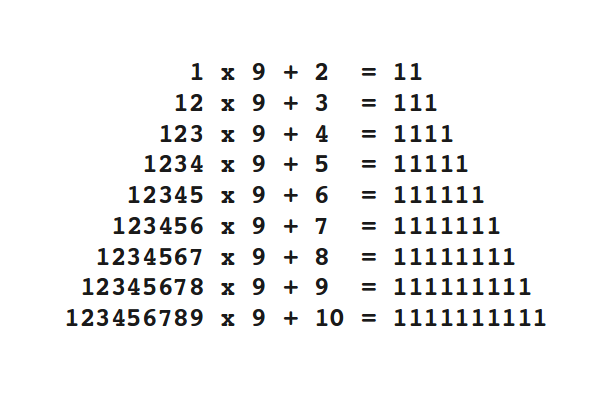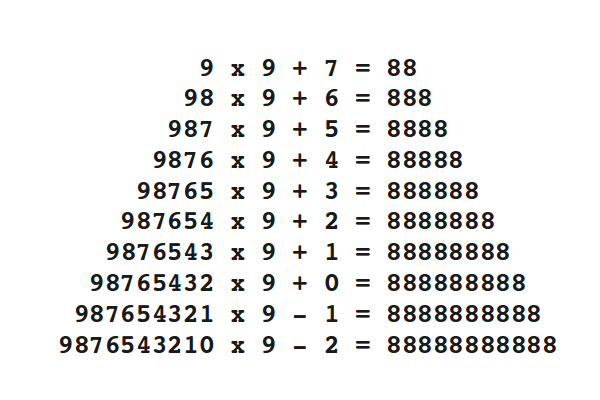I recently read an article about the mathematics of beauty. Researchers found out that beauty is not in the eye of the beholder, and that beauty can indeed be quantified. If you want to read the article, here is a link.

Now, if it is possible to describe what beauty is using mathematical formulas, maybe it is also possible to look at the issue the other way around. Can math itself be considered beautiful or ugly? I did find an answer to this question by the English mathematician G. H. Hardy (1877-1947):

“The mathematician’s patterns, like the painter’s or the poet’s must be beautiful; the ideas, like the colours or the words must fit together in a harmonious way. Beauty is the first test: there is no permanent place in this world for ugly mathematics.’’ G. H. Hardy

Imagine that you are working on a math problem. You do your calculations and you calculate an answer to the problem. Let’s say that the solution turns out to be 23.119231. Someone else works on the same math problem and also comes up with an answer. In this case turns out to be exactly 1. Evidently one of you two made a calculation mistake. Which answer do you tend to trust more, the 23.119231 or the 1? Which one of the two is more likely to be correct? Many people would distrust the 23.119231 much more because it is an “ugly” answer. The 1 is simply the more “beautiful” answer. But from a mathematical standpoint, there is no real reason why the 1 should be given a preference. Seen from a purely statistical viewpoint, both numbers are equally likely to occur. Still, many of us prefer the 1. Let’s think back a bit and be honest, have we not all once said the words “this is not a beautiful solution”, “this answer doesn’t look nice” or “what a nice result” when solving math problems? Cuolt it be that we are using beauty as a “truth test”? Do we consider a beautiful answer more likely to be correct?

Pythagoras (c. 570-c. 495 BC), for example, was very unhappy about the discovery of irrational numbers. These are numbers that can not be expressed in simple ratios of two natural numbers. Irrational numbers have an infinite number of decimal places and these do not repeat. Pythagoras considered irrational numbers so “ugly” (even though he probably did not use this term), that he considered the existence of irrational numbers as a flaw in nature.

I wonder now, how does beautiful math look like? And what is ugly math? Isn’t math simply math? How can we ascribe qualities such as beauty and ugliness to abstract concepts such as math, or even the sciences, I wonder. Now, I think that a mathematical formula or scientific theory is beautiful if it fulfills two criteria:

• The formula, proof, theory or experiment must be simple. Simplicity is an important component of beauty.
• It must also possess much explanatory power (a clumsy term, I know. But I couldn’t come up with a better term). With explanatory power I mean that it must be able to link or connect seemingly unrelated concepts. The explanatory power of a mathematical formula (or even a scientific theory) is its ability to explain how two seemingly unrelated ideas are connected.

In summary:

beauty = simplicity * explanatory power

Isn’t this a beautiful formula? Just in case you are worried that I’m really getting carried away here, I’m not being very serious here, but a little bit maybe….. The formula 1+1=2 may be very simple, but it really does not explain very much. It does not really connect different concepts together. So the overall beauty of the formula is quite low. In contrast, I consider Albert Einstein’s famous equation E=mc² a very beautiful equation. The equation links mass, energy and the speed of light, three at first sight seemingly completely unrelated concepts, in a simple straight forward formula.

Still, Einstein’s formula is topped by Euler’s Identity (this is the name of the formula). This one is considered by many people to be “greatest equation ever” (PhysicsWorld, 2004), and Paul Nahin from the University of New Hampshire stated that Euler’s Identity is “the gold standard for mathematical beauty.” He even dedicated a whole 400-page book to the formula.

Euler’s identity is a remarkably simple formula. It links five important constants: Euler’s constant e, pi, imaginary number i, 0 and 1. The formula is considered beautiful not only because of its simplicity. It is considered beautiful because it links five seemingly unrelated constants together. What do imaginary numbers, pi, e, 0 and 1 have to do with each other? They seem to be completely unconnected in our everyday life and experience! Yet, Euler’s formula is able to uncover a connection. It therefore possesses a high explanatory power on how these numbers are related to each other.

The concept of beauty is not only limited to math, but can also be found in related areas such as in computer science. Computer programmers don’t use the word “beauty”, however, when they want to characterize an algorithm that they devised. They like to use the term “elegant”. A computer programmer who comes up a very effective, original and short solution to a complicated problem, then the programmer would say: “I’ve found an elegant solution to the problem.”. Even mathematicians use the term “elegance” when they want to characterize short and effective mathematical proofs.

But maybe simplicity and explanatory power (I still don’t like this term…) are not really sufficient in characterizing beauty after all. When I look at a beautiful painting or listening to beautiful music, then I’m not really judging their ability to explain something. A beautiful piece of art is simply pleasing to look at. You just enjoy it for its own sake.

In the middle ages, astronomers assumed that the earth is in the center of the universe and that the sun and the planets revolve around earth. The model was indeed capable of explaining the position of the planets, but the model was very complex as well. The Polish astronomer Nicolai Copernicus considered this model “neither sufficiently absolute nor sufficiently pleasing to the mind.” Now this gets me thinking again. Maybe beauty is simply the ability to delight the senses and to please the mind?

Beauty = Ability to please one’s mind

To conclude: Why am I worried about the issue of beauty in the first place? Why bother? I’m in the search for truth, you know. If I discover beauty, then I also found truth. Really.

Truth = Beauty

“Beauty is truth, truth beauty,” – that is all
Ye know on earth, and all ye need to know. – John Keats (in: Ode to a Grecian Urn)